Nice find Mikehmikeh wrote: 07 Sep 2018, 12:43 Another example of Pythagoreanism being used in relation to the tarot, I think, is in Piscina's Discorso, 1565 Piedmont, although only about the four suits of Swords, Batons, Cups, and Coins. It sounds more Pythagorean in the original than in the published translation. He says:ora perchè più presto in numero quadernario che in altro potremo dire come in più perfetto anzi perfettissimo de gl'altri si come fra tutti & ispetialmente moderni il dottissimo Ficino ha scritto nel argomento fatto sopra il Timeo di Platone dal XX. Fino al 24. Cap.
Re: Le Tarot arithmologique - la séquence 1+4+7+10 = 22
642Thanks Mike. You are absolutely right, "quaternary" would be a better translation than merely "four". Certainly more informative, and worthy of a better note, like you have provided. Hopefully we'll find it in Ficino on Timaeus.
This is another demonstration of the value of including the original text beside any translation. Sometimes a comparison will improve the translation and deepen the understanding of the text simultaneously. Besides the often superficial, if sometimes aesthetically valuable, stylistic criticisms, I mean.
I think you are probably right that Piscina is thinking of the tetraktys. I'll look up how the word works; in the meantime, here are some suggestive points from Liddell and Scott's Greek English Lexicon -
 Here is a translation of the Oath referred to in Liddell and Scott, by John Dillon in The Heirs of Plato, A Study of the Old Academy (347-274 BC), OUP, 2003, p. 101
Here is a translation of the Oath referred to in Liddell and Scott, by John Dillon in The Heirs of Plato, A Study of the Old Academy (347-274 BC), OUP, 2003, p. 101
"Nay, by the man I swear who bequeathed to our head the Tetraktys,
Fount containing the roots of nature ever-flowing (physis aenaos)."
This is another demonstration of the value of including the original text beside any translation. Sometimes a comparison will improve the translation and deepen the understanding of the text simultaneously. Besides the often superficial, if sometimes aesthetically valuable, stylistic criticisms, I mean.
I think you are probably right that Piscina is thinking of the tetraktys. I'll look up how the word works; in the meantime, here are some suggestive points from Liddell and Scott's Greek English Lexicon -

"Nay, by the man I swear who bequeathed to our head the Tetraktys,
Fount containing the roots of nature ever-flowing (physis aenaos)."
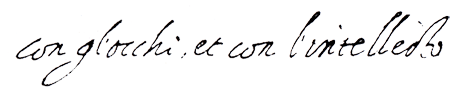
Re: Le Tarot arithmologique - la séquence 1+4+7+10 = 22
643The only explanation I can find so far for the “-ktys” is that it is from the word “traktos”, an ancient wax writing board. So by this explanation “tetraktus” is a Pythagorean neologism, a melding of “tetra-“ with “traktos”.
This etymology is on this page, with the relevant statement bolded by me –
http://www.greekalphabeta.com/learn-abo ... u-300.html
“Tetraktus (τετρακτύς) is the tetraktys, the Pythagorean name for the sum of the first four numbers, which equals 10 (1 + 2 + 3 + 4 = 10).
In geometry, the number one represents the point, two represents the line, three represents the surface, and four represents three-dimensional forms.
The shape of the first four letters of the alphabet reflect these geometric concepts:
1-Α comes to a point
2-Β consists of two parts, the definition of a line
3-Γ rises up to a horizontal surface (Ge)
4-Δ forms a triangle reminiscent of the pyramids.
The tetraktus (τετρακτύς) (tetraktys) is illustrated below.
http://en.wikipedia.org/wiki/Tetractys
http://ouchmath.wordpress.com/2011/03/1 ... functions/
(It is of interest that traktos (τρακτός), the second part of the word tetraktus (τετρακτύς), means a white, bleached wax, a malleable substance that can be used to create three-dimensional forms.)
The Pythagoreans would swear their oath on the tetraktrun, “which contains the fount and root of eternal nature.”
(Aëtius (Άέτιος) (I, 3,8) quoted by Patricia Curd, Daniel W. Graham. The Oxford Handbook of Presocratic Philosophy(Oxford and New York: Oxford University Press, 2008) 480.)
http://books.google.com/books?id=14muxt ... us&f=false
The Pythagorean oath in Greek is as follows:
οὕ, μά τόν άμετέρα γενεᾶ παραδόντα τετρακτύν,
παγάν άενάου φύσεως ῥιζώματ' ἕχουσαν.
(Mattei, ό. π., σ.88.) (quoted in Tsampoukos ΠΥΘΑΓΟΡΙΣΜΟΣ, ΕΝΑΣ ΜΑΘΗΜΑΤΙΚΟΣ ΚΟΣΜΟΣ page 11)
“In all: divine-connection stretch up to mother-creator in gratitude for the tetraktun,
All eternal physics’ mother-root within-contained.” (Translated by Catherine Proppe, 2012.)
Another version of this oath is:
ναί μά τόν άμετέρα ψυχᾷ παραδόντα τετρακτύν,
παγάν άενάου φύσεως ῥιζώματ' ἕχουσαν. (Mattei, ό. π., σ.88.)”
This etymology is on this page, with the relevant statement bolded by me –
http://www.greekalphabeta.com/learn-abo ... u-300.html
“Tetraktus (τετρακτύς) is the tetraktys, the Pythagorean name for the sum of the first four numbers, which equals 10 (1 + 2 + 3 + 4 = 10).
In geometry, the number one represents the point, two represents the line, three represents the surface, and four represents three-dimensional forms.
The shape of the first four letters of the alphabet reflect these geometric concepts:
1-Α comes to a point
2-Β consists of two parts, the definition of a line
3-Γ rises up to a horizontal surface (Ge)
4-Δ forms a triangle reminiscent of the pyramids.
The tetraktus (τετρακτύς) (tetraktys) is illustrated below.
http://en.wikipedia.org/wiki/Tetractys
http://ouchmath.wordpress.com/2011/03/1 ... functions/
(It is of interest that traktos (τρακτός), the second part of the word tetraktus (τετρακτύς), means a white, bleached wax, a malleable substance that can be used to create three-dimensional forms.)
The Pythagoreans would swear their oath on the tetraktrun, “which contains the fount and root of eternal nature.”
(Aëtius (Άέτιος) (I, 3,8) quoted by Patricia Curd, Daniel W. Graham. The Oxford Handbook of Presocratic Philosophy(Oxford and New York: Oxford University Press, 2008) 480.)
http://books.google.com/books?id=14muxt ... us&f=false
The Pythagorean oath in Greek is as follows:
οὕ, μά τόν άμετέρα γενεᾶ παραδόντα τετρακτύν,
παγάν άενάου φύσεως ῥιζώματ' ἕχουσαν.
(Mattei, ό. π., σ.88.) (quoted in Tsampoukos ΠΥΘΑΓΟΡΙΣΜΟΣ, ΕΝΑΣ ΜΑΘΗΜΑΤΙΚΟΣ ΚΟΣΜΟΣ page 11)
“In all: divine-connection stretch up to mother-creator in gratitude for the tetraktun,
All eternal physics’ mother-root within-contained.” (Translated by Catherine Proppe, 2012.)
Another version of this oath is:
ναί μά τόν άμετέρα ψυχᾷ παραδόντα τετρακτύν,
παγάν άενάου φύσεως ῥιζώματ' ἕχουσαν. (Mattei, ό. π., σ.88.)”
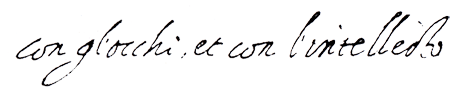
Re: Le Tarot arithmologique - la séquence 1+4+7+10 = 22
644BOUGEAREL Alain wrote: 07 Sep 2018, 13:16Nice find Mikehmikeh wrote: 07 Sep 2018, 12:43 Another example of Pythagoreanism being used in relation to the tarot, I think, is in Piscina's Discorso, 1565 Piedmont, although only about the four suits of Swords, Batons, Cups, and Coins. It sounds more Pythagorean in the original than in the published translation. He says:ora perchè più presto in numero quadernario che in altro potremo dire come in più perfetto anzi perfettissimo de gl'altri si come fra tutti & ispetialmente moderni il dottissimo Ficino ha scritto nel argomento fatto sopra il Timeo di Platone dal XX. Fino al 24. Cap.
Very interesting four the relation 4 emblèmes
PS
I do not forget that there is a pythagorean relation between the 22 and the 220 emblems of the 4 suits
In each of the 4 suits :
1+2+3+4+5+6+7+8+9+10 = 55
That is 220 = 55x4
So the 4 suits = 220 emblems
and the 22 allegorical subjects are , in pythagorean terms, in clear and unambiguous relation.
And this relation from the 22 to the 220 is the Tetractys : 22x10 = 220!
Last edited by BOUGEAREL Alain on 07 Sep 2018, 17:54, edited 7 times in total.
Re: Le Tarot arithmologique - la séquence 1+4+7+10 = 22
645Ross G. R. Caldwell wrote: 07 Sep 2018, 14:30 The only explanation I can find so far for the “-ktys” is that it is from the word “traktos”, an ancient wax writing board. So by this explanation “tetraktus” is a Pythagorean neologism, a melding of “tetra-“ with “traktos”.
This etymology is on this page, with the relevant statement bolded by me –
http://www.greekalphabeta.com/learn-abo ... u-300.html
“Tetraktus (τετρακτύς) is the tetraktys, the Pythagorean name for the sum of the first four numbers, which equals 10 (1 + 2 + 3 + 4 = 10).
In geometry, the number one represents the point, two represents the line, three represents the surface, and four represents three-dimensional forms.
The shape of the first four letters of the alphabet reflect these geometric concepts:
1-Α comes to a point
2-Β consists of two parts, the definition of a line
3-Γ rises up to a horizontal surface (Ge)
4-Δ forms a triangle reminiscent of the pyramids.
The tetraktus (τετρακτύς) (tetraktys) is illustrated below.
http://en.wikipedia.org/wiki/Tetractys
http://ouchmath.wordpress.com/2011/03/1 ... functions/
(It is of interest that traktos (τρακτός), the second part of the word tetraktus (τετρακτύς), means a white, bleached wax, a malleable substance that can be used to create three-dimensional forms.)
The Pythagoreans would swear their oath on the tetraktrun, “which contains the fount and root of eternal nature.”
(Aëtius (Άέτιος) (I, 3,8) quoted by Patricia Curd, Daniel W. Graham. The Oxford Handbook of Presocratic Philosophy(Oxford and New York: Oxford University Press, 2008) 480.)
http://books.google.com/books?id=14muxt ... us&f=false
The Pythagorean oath in Greek is as follows:
οὕ, μά τόν άμετέρα γενεᾶ παραδόντα τετρακτύν,
παγάν άενάου φύσεως ῥιζώματ' ἕχουσαν.
(Mattei, ό. π., σ.88.) (quoted in Tsampoukos ΠΥΘΑΓΟΡΙΣΜΟΣ, ΕΝΑΣ ΜΑΘΗΜΑΤΙΚΟΣ ΚΟΣΜΟΣ page 11)
“In all: divine-connection stretch up to mother-creator in gratitude for the tetraktun,
All eternal physics’ mother-root within-contained.” (Translated by Catherine Proppe, 2012.)
Another version of this oath is:
ναί μά τόν άμετέρα ψυχᾷ παραδόντα τετρακτύν,
παγάν άενάου φύσεως ῥιζώματ' ἕχουσαν. (Mattei, ό. π., σ.88.)”
Re: Le Tarot arithmologique - la séquence 1+4+7+10 = 22
646I like this observation Ross
(It is of interest that traktos (τρακτός), the second part of the word tetraktus (τετρακτύς), means a white, bleached wax, a malleable substance that can be used to create three-dimensional forms.)
(It is of interest that traktos (τρακτός), the second part of the word tetraktus (τετρακτύς), means a white, bleached wax, a malleable substance that can be used to create three-dimensional forms.)
Re: Le Tarot arithmologique - la séquence 1+4+7+10 = 22
647A recent author, Viltanioti, mentions that Iamblichus considered Tetraktys to be a neologism invented by Pythagoras, but in a brief survey of the historical literature considers that the real etymology is obscure.
Irini-Fotini Viltanioti
L’harmonie des Sirènes du pythagorisme ancien à Platon
De Gruyter, 2015
https://books.google.fr/books?id=s_U-Cw ... 22&f=false

Irini-Fotini Viltanioti
L’harmonie des Sirènes du pythagorisme ancien à Platon
De Gruyter, 2015
https://books.google.fr/books?id=s_U-Cw ... 22&f=false

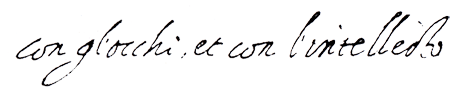
Re: Le Tarot arithmologique - la séquence 1+4+7+10 = 22
648The book by Armand Delatte cited by Viltanioti is Etudes sur la littérature pythagoricienne, first published in 1915 (Viltanioti uses a 1974 reprint, but it is the same pagination). See Chapter VIII, "La Tétractys pythagoricienne" (pp. 249ff). Given that it was a century between Delatte and Viltanioti, Delatte's études seem to remain the standard reference for this question.
https://www.notesdumontroyal.com/document/401r2.pdf
https://www.notesdumontroyal.com/document/401r2.pdf
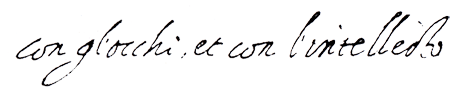
Re: Le Tarot arithmologique - la séquence 1+4+7+10 = 22
649Your insight bears fruit, Mike -
(Google phrase searching the string "numero quadernario" "timeo" "platone" "ficino")
I haven’t found the source in Ficino yet, but like Piscina this author uses him, showing that he identifies this “quadernario” with the Tetraktys:
Romano Alberti, Origine et progresso dell’academia del dissegno, de pittori, scultori, & architetti di Roma. – Pavia, 1604.
« Marsilio Ficino, per dimostrare la verità delle cose sopra il timeo di Platone, dice che il numero quadernario contiene sotto di se il primo numero pari, il primo dispari, e perciò li elementi concorrano alla generatione, & che non devono essere più che quattro, ne meno che quattro, per palesare parimente la verità, del tutto dice Marsilio Ficino, imitando la Tettratti di Pitagora, come nell’istessa quadratura ci si trova l’universal virtù d’ogni cosa… »
https://books.google.fr/books?id=QpdbAA ... 22&f=false
(Google phrase searching the string "numero quadernario" "timeo" "platone" "ficino")
I haven’t found the source in Ficino yet, but like Piscina this author uses him, showing that he identifies this “quadernario” with the Tetraktys:
Romano Alberti, Origine et progresso dell’academia del dissegno, de pittori, scultori, & architetti di Roma. – Pavia, 1604.
« Marsilio Ficino, per dimostrare la verità delle cose sopra il timeo di Platone, dice che il numero quadernario contiene sotto di se il primo numero pari, il primo dispari, e perciò li elementi concorrano alla generatione, & che non devono essere più che quattro, ne meno che quattro, per palesare parimente la verità, del tutto dice Marsilio Ficino, imitando la Tettratti di Pitagora, come nell’istessa quadratura ci si trova l’universal virtù d’ogni cosa… »
https://books.google.fr/books?id=QpdbAA ... 22&f=false
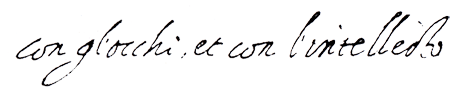
Re: Le Tarot arithmologique - la séquence 1+4+7+10 = 22
650mikeh wrote: 07 Sep 2018, 12:43 Another example of Pythagoreanism being used in relation to the tarot, I think, is in Piscina's Discorso, 1565 Piedmont, although only about the four suits of Swords, Batons, Cups, and Coins. It sounds more Pythagorean in the original than in the published translation. He says:And the published translationora perchè più presto in numero quadernario che in altro potremo dire come in più perfetto anzi perfettissimo de gl'altri si come fra tutti & ispetialmente moderni il dottissimo Ficino ha scritto nel argomento fatto sopra il Timeo di Platone dal XX. Fino al 24. Cap.A literal reading of "numero quadernario" would be "quaternary number", a Pythagorean way of talking although not exclusively so, since it is seen in Euclid, etc. But in the number theory handed down from Euclid four is decidedly not a perfect number. A perfect number is one that is the sum of its divisors, including 1or half the sum of its divisors if the number itself is included. So the first perfect number is 6, which is 1 + 2 + 3, or half of 1+2 +3+6. The next one is 28, which is 1+2+4+7+14. The divisors of 10 are 1+2+5 = 8, which falls short.Now why in the number of four and not another we can say because it is more perfect than all the others. Among all, and especially modern writers, this has been explained by the very learned Ficino in his discussion on Plato's Timaeus from chapters XX to 24.
Why would Piscina call 4 a perfect number? To my knowledge Plato does not say anything of the sort in the Timaeus, however much otherwise that work shows much Pythagorean influence. But Ficino in his commentaries brings to bear all of his learning to the text in question. Perhaps the answer is somewhere in Ficino's book. There is an English translation of Ficino's Commentary on Plato's Timaeus, but it is not available in any library near me. I am hoping to get it from Interlibrary Loan. Until then, I offer the following speculation.
Aristotle in his Metaphysics Book 1 Section 5 discusses the Pythagoreans. Among other things he makes fun of them, saying they invent things when their theory requires it. So we have, in the medieval Latin translation available online (http://www.logicmuseum.com/wiki/Authors ... #Chapter_5:In W. D. Ross's translation:Dico autem puta quoniam perfectus denarius esse videtur et omnem comprehendere numerorum naturam, et quae secundum celum feruntur decem quidem esse dicunt. Solum autem novem existentibus manifestis, ideo antixthonam decimam faciunt.Aristotle is no mathematician, and the Greek word translated as "perfect", τέλειον, teleios, also means "brought to its end, finished", which is surely the sense here (https://www.biblestudytools.com/lexicon ... leios.html). After ten (deka), the next number is "10+1", in Greek deka + en, or 'hendeka", and so on (http://phrontistery.info/numbers.html). Actually, twenty was not a compound of "two" and something meaning "tens", but something new, "eikosi". But that is a small point. The numbers in Greek did repeat one through nine every ten of them.E.g. as the number 10 is thought to be perfect and to comprise the whole nature of numbers, they say that the bodies which move through the heavens are ten, but as the visible bodies are only nine, to meet this they invent a tenth—the ‘counter-earth’.
Piscina does not say that ten is a perfect number; he says "four". My hypothesis is that he is thinking of the "tetraktys", a uniquely Pythagorean notion, a triangle made of dots that shows ten as the sum of the first four numbers. While the tetraktys is 10, it also contains within it "tetra", meaning 4 (what -ktys meant, I have no idea). According to Wikipedia the Pythagoreans also called the tetraktys "the Mystical Tetrad".
That is my hypothesis for how 4 becomes a perfect number, an eminently Pythagorean notion somewhat lost in translation. If I am able to get the Ficino, I will say more.

Also an unpublihed artcle : the 56 cards a Tetractys game
https://docs.google.com/document/d/1_am ... 631RI/edit
