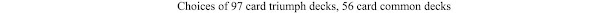I have put off translating this note of Fanco’s because every time I looked at it in Italian, I couldn’t follow the argument. If I couldn’t follow it, how could I translate it? Not only that, it would be a great personal embarrassment to me to get it wrong. It is a matter of solving what we used to call in middle school (junior high school, we called it) a “story problem”. I used to be good at such things. If these days I can’t even follow the solution to a problem in simple arithmetic, what does that say about the state of deterioration of my brain?

However I have been studying Pythagorean number theory a bit lately. That might help. So at Huck’s urging (viewtopic.php?f=11&t=1100#p18158) I am taking the plunge. After many hours of puzzling over it, I think it is Franco who is confused. That is a rather strong claim, I know, and another reason for hesitating to translate it. One of us is wrong, and I will be even more embarrassed if it is me. But I can’t let fear of shame and dishonor stand in the way of truth. In another post I will try to explain what he is doing (for the arithmetically challenged) and what I think is wrong. Below, in the translation, as usual comments in brackets are by me, and the page numbers correspond to the original, "1477: Bologna – Aritmetica per carte e trionfi", at http://www.naibi.net/A/323-BONOZZI-Z.pdf.


1477 Bologna: Arithmetic for cards and triumphs

Franco Pratesi – 09.06.2014

Introduction

The idea for writing this note comes from rereading an article published more than a century ago, which directed attention, among other things, to an important Bolognese document of 1477. (1) A copy of the original article with some comments is even available on the Internet. (2) It is a well known text variously commented on by several experts. Some deductions derived from that information seem to have to be revised; others are better understood with a different assessment; others seem to me would require further thought and reflection.

The justification for submitting these reflections to the attention of the experts is that ultimately I have provided many new numbers for card games that should be granted to me from reasoning a bit on the old numbers supplied by others.

The Data

The earliest documents found in the archives of Bologna and published by Orioli represented very early evidence, such as to lead many experts to consider Bologna a very important center for the production of playing cards, beginning from their first diffusion. It is not easy to judge if such a conclusion is due to the fact that similar documentation in other cities and for previous periods. had not yet been found

But if we consider that the use of playing cards was already common for some time (for example in Florence at least from the beginning of 1377, so much so that the councilors concerned were induced to prohibit its further spread), the possible Bologna priority is reduced at most to the use of the woodcut as an important part of the production.

German card makers

From the point of view of woodcuts, still more significant is the large presence of German card makers among those documented in Bologna. It is known that the craft of woodworking for reproduction of pictures was very advanced in the regions of central and southern Germany and adjacent areas. It seems that all the oldest woodcuts that have come down to us stem from one area or another of so-called Mitteleuropa.

At this point it seems to me that the question is reduced to one alternative for resolution: did German playing card makers export to the rich Italian cities the production of playing cards or did they just flock to Italy because a production already widespread could take advantage of their technical expertise in woodworking?

Here the date becomes decisive, which is old only only in relation to others noted, but not so much as to suggest the introduction of new and original items. In my view the same phenomenon happened with playing cards as occurred with the manufacture of shoes: German shoemakers were very capable and easily found a new and abundant clientele in Italy, (3) but it is not legitimate to draw the consequence that in our cities shoes were introduced by German shoemakers.

Naibi in Florence

Even before woodcuts and the Florentines’ use of naibi and cards, the way appears to have been prepared with drawing and painting on pieces of parchment. In this regard, in the article in question we read a cursed affirmation: Naibi. E questa stessa parola si trova spesso ricordata sul principio del secolo XV in atti notarili fiorentini, dove si descrivono le carte quali foglietti in pergamena artisticamente figurati e dipinti.
(Naibi. And this same word is often mentioned, in the beginning of the

2
15th century, in Florentine notary acts, which describe cards as sheets of parchment, artistically depicted and painted.[/i]

I do not know Orioli’s reliability, but I have seen that the archives that he frequented were Bolognese and not Florentine. I do not think he spent much time in Florentine archives; perhaps the only important news stemmed only from word of mouth among archivists of the era.

Twenty years ago I wrote in this regard: (4)

If it were possible to document that claim with specific references, related in particular to the end of the fourteenth century, one would have a very useful confirmation of the value of this type of naibi. Unfortunately, the number of Notarial codices in the Pre-cosimian Archives is so high that it is virtually impossible to examine them in a comprehensive manner. Furthermore, the notarial writing of the time is much trickier to decipher than those prevailing in other documents, and my reading ability is often insufficient. It is therefore no wonder if the examination of a small sample of notarial codices of the fourteenth century (where one must also have been able to find some citations of naibi in the years immediately preceding 1377) provided a disappointing result: I found there a few inventories of goods and none that contained naibi.

Since then I have flipped through some other notarial registers, but without finding anything in the archival collection; better to turn to Bologna, for now.

The numbers of cards and of triumphs

This is precisely the point that is making me revisit the subject after a long time. I remembered well the fundamental concept of this document published by Orioli, a contract of Peter Bonozzi of Bologna, with whom he undertook in 1477 to secure his son, a card maker, a commitment to produce cards and triumphs exclusively for the client Roberto di Blanchelli under precise conditions.

Of the figures reported then, in 1908, one can get more related important information, as follows.

• 1) both cards and triumphs were used for playing [giocare];
  
  2) cards were only 40, triumphs 60;
  
  3a) production occurred in groups of 125 decks of cards, or in the case of a smaller number of groups also including packs of triumphs, in an "equivalent" manner, ie, with a same total number of cards.
  3b) each card, whether belonging to cards or triumphs, required roughly the same commitment to work and the same raw materials, so that differences in price thus did not exist (a rasone de carta per carta debba essere pagato come de le carte e non più [because card for card should be paid as cards and no more].)

It would seem that we can thus obtain complete information, expressed quantitatively with exact numbers. The issue, however, is that these numbers are almost never precise and moreover the only exact number that appears in the original document is rather enigmatic.

We will start precisely from the number registered with accuracy: 125 decks of cards. This is the only number given for the quantity of cards in the old document, published for the first time in 1908; Orioli inserted the others in 1908 on his own initiative.

Personally, I have always found, for various periods, that the manufacture and sale of playing cards was made taking as a unit a dozen decks. Indeed, they usually had exact figures, i.e. expressed in whole numbers of lire, only for dozens of packs, while the price of a single pack had to be expressed using all the small change available after lire, namely either soldi, a twentieth of a lire, or denari, twelfths of a soldo

3
In short, if this document had read, instead of 125, a number of 120 decks, I would be more at ease, and even more if I had found 144, a dozen dozens, one gross.

Despite everything, this number 125 must be accepted, and indeed will be taken as a fixed point of departure for further calculations. There remains only a certain underlying skepticism about why that precise number of decks was chosen as the basis of this production contract.

The fundamental question which confronts us now is as follows. If instead of producing cards they produced triumphs, how many decks of triumphs corresponded to 125 decks of cards?

With the elements available, it is an elementary school arithmetic problem that would only have the difficulty for the pupil of giving as its solution a fractional number of packs, which is not very nice in any elementary school.

Orioli in fact tells us that the cards were 40 and triumphs 60 and the poor student is thus finds that to 125 decks of cards correspond approximately 83.33 decks of triumphs; to have a more accurate result one would have made oneself familiar beforehand with the numbers of the period (also themselves poorly suited to counting playing cards).

It must, however, be noted that we are using numbers from different sources: the number 125 is of
1477, the numbers 40 and 60 are of 1908! Not to say that the integers are transformed over the years, but only that the problem would be proposed more correctly if all three numbers were taken from 1477 and the same author.

Instead, the original contract tells us precisely nothing about the number of cards in the common deck, or of that of triumphs; it tells us only that the two numbers were different and makes us understand clearly that the number of triumphs was greater than that of cards, but does not specify the difference.

Everything here can be verified in the passage in question, copied as follows.

Item che el prefato ser Roberto sia obligato dare e pagare al prefato maestro Pietro o a suo figliolo in suo nome soldi diexedotto de quattrini per ogni centovinticinque para de carte, o vero triumphi para tanto manco de centovinticinque para, quanto gette el numero de le carte che ha più li iochi de li triumphi da quilli de le carte.

(Item that the aforesaid Mr. Roberto is obligated to give and pay to the aforesaid Master Pietro or his son in his name eighteen soldi of money for each 125 packs of cards, or true triumphs sufficiently less than for 125 packs, in so far as the number of the cards is more of Triumphs than of cards.)

Now it's up to us to reconstruct the situation and re-propose the problem in terms as correct as possible, or at least convincing. The trouble is that great uncertainty is encountered in the possible data.

As far as we know today, the common deck could have been formed of 40 cards, as Orioli affirms, but also by 32, 48, 52, or 56, and above all that of triumphs could have 60, again according to Orioli, or 62, as in the Bolognese Tarocchino, or 70, as in some testimonies of the time, or 78, as common subsequently in tarot cards, or even 96 if not 97, as in minchiate. Other numbers would have been possible for both decks.

In short, we can have fun in formulating the most varied possible combinations of the two numbers of cards, possibly through looking at pairs with a simple relationship between them, so as to facilitate the achievement of the final goal: to obtain whole numbers of packs, with the same total number of cards, producing both cards and triumphs.

However, by the end of the process, or even before starting it, we must ask a question in certain summary directions. Why in the contract itself is the numerical correspondence between cards and triumphs not very precisely expressed in an explicit manner? Even here I do not find only one sure answer, and thus I try to advance several hypotheses, so that the reader can choose the one that convinces him the most.

The simplest explanation I see is this: the card maker did not produce only cards or only triumphs, but in practice produced them together and on top of that in relatively variable amounts from time to time depending on demand or availability. Then there is no sense in making explicit the total number of decks of triumphs, because instead of 125 decks of cards he could have for example as numbers of decks (but not using these fictitious numbers for other accounts!) at one time 90 of cards and 30 of triumphs, another time 80 of cards and 35 of triumphs, and yet another, 70 of cards and 40 of triumphs, so that it would be

4
difficult to provide a list of all possible cases. Better to adjust the count [conte] from time to time.

Another possible explanation is that the two basic numbers were not fixed. The number of cards in the two decks could vary according to their destination. Out of place would be "my" Florentine numbers that could have been simply 48 and 96, which would still leave our schoolboy faced with an inconvenient result of 62.5 packs of triumphs instead of 125 of cards, the only safe number. However, other different compositions could have been produced to send to other cities.

The two proposed explanations so far are very different from each other, but share a common element: both suggest a possible reason not to write a second number in the contract, where in fact none appears.

However, anyone will be able to imagine a third easy solution: the number of cards in the common deck and in the triumphs was not only fixed, but also so well known to all that there was no need to write it explicitly in the contract, as evident to anyone reading it. We will try to go that route.

A key starting point for the search is as follows: if they produced both cards and triumphs there had to be a simple relationship between the two decks of cards, so that there were quite frequent coincidences in the total number of cards forming different numbers of related decks.

In other words, it would not be at all be convenient to produce from time to time cards in equal number, but corresponding to partial decks! If X decks of cards are produced together with Y decks of triumphs, the situation requires that X and Y be whole numbers; it is much better, the more they are found, these X and Y integers, for the same total number of cards.

Then the problem is no longer elementary school, even considering the existing uncertainty about the number of cards in their decks. But regardless of the cards of the two numbers in two different decks, it is from studying what the "comfortable" number of packs to produce is. We go to middle school and seek the possible X decks of cards and Y decks of triumphs.

The starting point is that X must be 125 if Y is zero. The total number of cards will be clearly XNc where I indicate with Nc the number, undetermined for now, of cards in the deck of regular cards. I indicate with Nt the number of cards in a deck of triumphs. Now we want the total number of cards to remain constant, albeit mixing decks of cards and triumphs.

This can be expressed simply as follows:



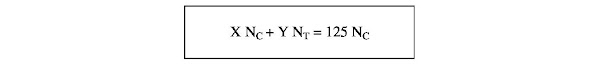
If Y = 0, that is, we produce only cards, X will be 125, as we knew from the start. But we can do the opposite, producing all triumphs and no decks of cards, that is, put X = 0. So once again we get a useful result:



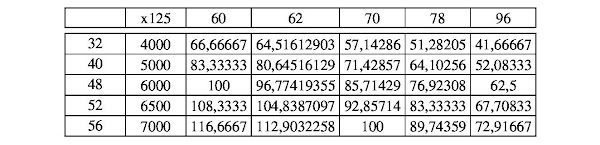
But now we have put in addition the condition that Y must be an integer, because we do not want unuseful fractions of decks. We can then proceed by trial and error, using the most plausible values suggested above for both Nc and Nt, so as to verify what are able to be provided as Y integers.

One such attempt was made in the following table:

5


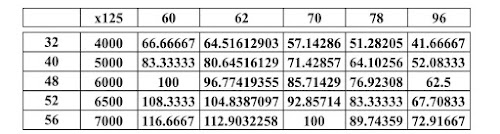
In the first column are "plausible" values of Nc' in the second these have been multiplied by "our" number of 125. Subsequent columns show the relationships 125 (Nc/Nt) for "plausible" Nt values as indicated on the top row.

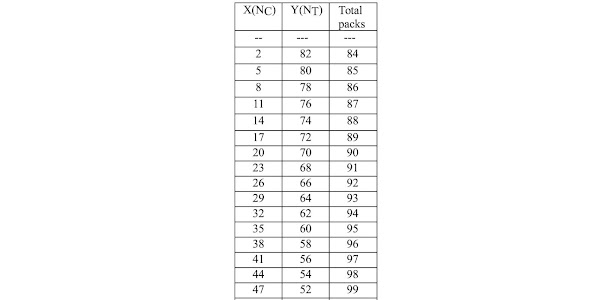
We wanted Y to be an integer and in the table there are only two pairs of Nc and Nt that prove suitable. Unless introducing other plausible numbers of cards are introduced for the two decks, with those taken on a first attempt, there remain usable only 48/60 and 56/70.

In fact, it is precisely the starting number of 125 that is decisive for the entire procedure. Unfortunately for us, 125 is divisible only by 1 and 5; of the possible terms in n/5 with n an integer from 1 to 4, only 4/5 is a usable ratio in our case. So you find that to 125 decks of cards correspond 100 decks of triumphs.

In conclusion, it is found, by way of arithmetic, that triumphs were formed by the four usual suits of plus a fifth "suit" which had a number of cards equal to that of each of the four normal suits.

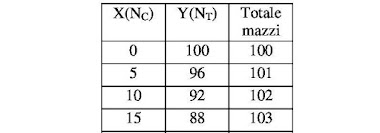
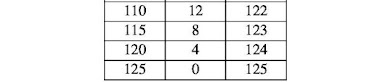
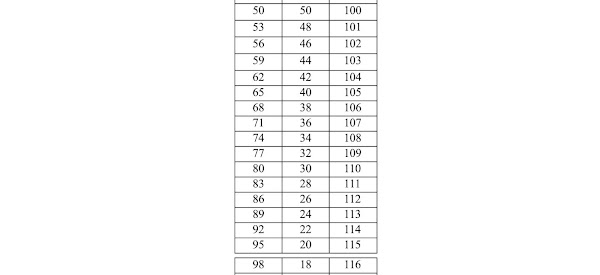
At this point we are ready to conclude the proceedings in the two directions taken. The first solution relates to the total numbers of decks that could be produced: the two extreme cases are clearly the 125 packs of only common cards, or, as we have now found, 100 packs of only triumphs.

All the possible intermediate cases for the numbers of mixed decks of cards and triumphs, including necessarily those in the range between 100 and 125, are listed in the following table and are numbers that increase one by one with the increase of the part of the common cards.



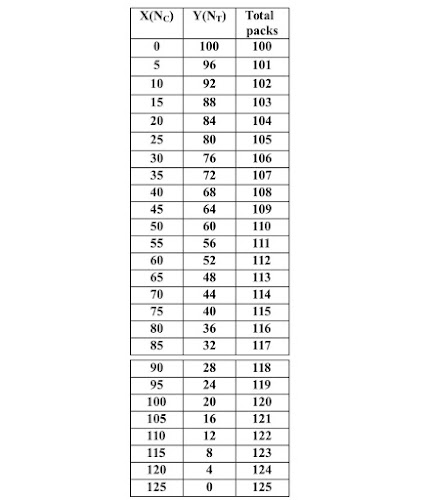
6
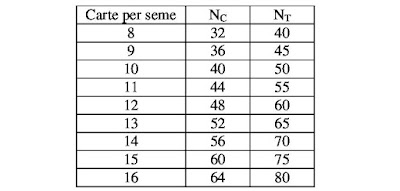
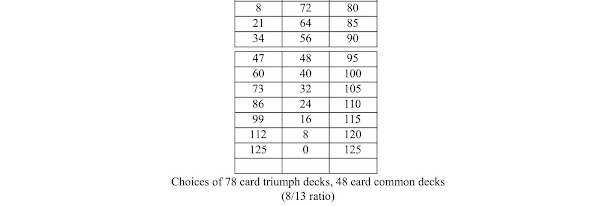
The second desired solution enters into the details of the cards contained in the two decks. The above table does not require precise numbers of cards in the two decks, but only that their relationship be of 4/5. Now we must examine which of the "plausible" numbers with 4/5 ratio are preferred.

In fact, the choice is rather limited, as shown in the following table:



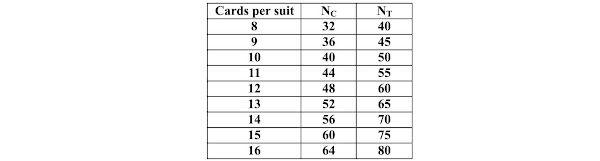
From what we know so far, the choice of the number 70 for the deck of triumphs does not create particular problems. There are even historical documents in Ferrara which read precisely of decks of 70 cards for the trumps. Also Lothar Teikemeier has been advancing for years the proposal of a primitive deck of triumph cards of the format 5x14. (5)


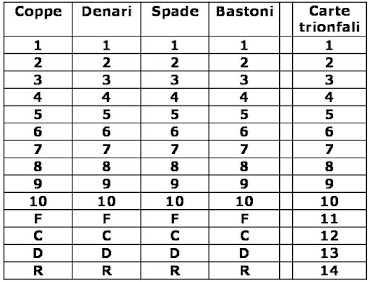
Figura 1 – Schema of the two decks discussed.

7
The question, if need be, concerns the common deck of 56 cards, which cannot be said to be common. After all, the idea of a deck of 56 cards is not entirely unique, because it corresponds in particular to the "normal cards" present precisely inside the tarot decks known from later times, with the number cards from 1 to 10 and the upper four figures: page, knight, queen, king. Among other things, the presence of a pack like that seems already documented in the sermons of San Bernardino, where all four figures are mentioned.

To me, however, it remains difficult to imagine an Italian “common” pack of 56 cards used in "common" games. In Italy, of the four figures as a rule only three are used, choosing either the knight or the queen by region. Also of the ten numeral cards some are eliminated; more often, at least in the sequence, those from 8 to 10 inclusive.

The production of decks of 56 cards then would suggest that they were produced so as to meet the requirements of different locations, in which, if desired, the deck could be reduced in various ways to conform it to the games and to the habits of local players.

The proposed solution does not appear a hundred percent convincing. However, the possible alternatives convince even less, except perhaps that of 12 cards per suit, with a series of only 12 triumphal cards. In this second case, it would probably be easier to accept suits of 12 cards, but the triumphal series of only 12 cards would present itself as a bit too limited from what little we know. The remaining possibilities are even less convincing, although some elements in favor taken in particular cases can be found for almost all, including the ultimate of the deck of 80 cards.

In particular, I am convinced that the above is derived directly from the choice of the number 125 of groups of decks. I do not think that that number is compatible with other solutions based on randomly chosen numbers for the two decks: with any two numbers the numerical coincidence which leads to an equal total number of cards becomes exceptional for different quantities of complete decks of the two types.

Before, I thought that that strange 125 could be the result of a mistake in the transcription of the document; Now, I see rather clearly the technical reasons that had led to its choice.

Conclusion

A 1908 article was re-examined in which important Bolognese documents for the history of playing cards were published for the first time. Data in the documents have been commented on again, as well as the presence in Bologna of German card makers and in Florence of naibi in notarial acts.

On the basis of the number of 125 decks of cards indicated as a reference for production, some arithmetic exercises have been carried out, in order to define the numbers of cards present in decks of [common[ cards and also of triumphs in 1477 Bologna. The two most plausible corresponding numbers were 56 and 70.

Notes

1. Emilio Orioli, Il libro e la Stampa, II (1908), 109-119.
2. http://trionfi.com/0/e/00/
3. Lorenz Böninger, Die deutsche Einwanderung nach Florenz im Spätmittelalter. Leiden-Boston
2006.
4. http://naibi.net/A/64-ORPELLI-Z.pdf
5. http://trionfi.com/0/f/

My comments on the above.

Let us go back to the beginning of the “story problem”. The starting point is that X must be 125 if Y is zero. Franco says:

The total number of cards will be clearly XNc where I indicate with Nc the number, undetermined for now, of cards in the deck of regular cards. I indicate with Nt the number of cards in a deck of triumphs. Now we want the total number of cards to remain constant, albeit mixing decks of cards and triumphs.

This can be expressed simply as follows:

If Y = 0, that is, we only produce cards, X will be 125, as we knew from the start. But we can do the opposite, producing all triumphs and no deck of cards, that is, put an X = 0. So once again you get a useful result:

These are the first two steps. However it seems to me that he has skipped a step and also mislabled his first equation. That one is not about what happens when Y is zero. It is the equation that governs the contract, whatever X and Y may be. To get the result when Y is zero, we put Y=0 in the first equation, i.e.

XNc + (0)Nt = 125 Nc.

Which reduces to:

XNc = 125 Nc.

In other words, the total number of cards is 125 times the total number of decks, if there are no triumph decks. Using small “x” as multiplication, this could be written more explicitly (although visually confusing) as

X x Nc = 125 x Nc

This is a very small point, which really makes no difference and perhaps is more confusing than what Franco wrote, but I think it is important to be precise.

Then the next result

Y = 125 (Nc/Nt)

is correct, for what happens when X = 0. It gives a formula for calculating how many triumph decks will result when there are no common decks at all. It depends on the ratio of the number of cards per suit for common decks to the number of cards for triumph decks.

Then he plugs in numbers for Nt and Nc, picking out of the thousands of possibilities the most plausible ones he can think of, based on what little we know from the literature (Remember, for those of us used to a different convention, that the comma is a decimal point.)

To get these strange numbers, first he calculates how many cards there will be if Y equals zero, for different plausible numbers of cards in the common deck. In this case it does not matter how many cards there are in triumph decks, because Y = 0. The formula is X = Nc x 125. Various plausible amounts for Nc are in the first column, with the total number of cards in the second column.

Then, for the remaining columns, he calculates how many cards there will be if X equals zero, for various plausible numbers of cards in common and triumph decks, using the formula Y = 125 (Nc/Nt). He takes the result of multiplying 125 by Nc and dividing by the number Nt, for various plausible numbers of cards in triumph decks. There are only two cases where the result is an integer, meaning that there are no cards left over.

He could also have achieved the same result by first taking the ratio of Nc to Nt and then multiplying that by 125. In the case where Nt = 60 and Nc = 48, the ratio is 48/60. If we divide both the numerator and denominator by 12, it reduces to 4/5. In the case where Nt = 70 and Nc = 56, the result, dividing both numerator and denominator by 14, the result is also 4/5. Taking that times 125, we know that in each case there will be exactly 100 triumph decks.

The next table works out what happens if, holding the ratio of 4/5 constant, we increase the number of decks. Here are just the beginning and end of that table, all I need for the illustration.


He finds that to get 101 decks, you have to increase the number of triumphs decks by 4, giving you 4 triumph decks and 95 common decks. It then proceeds in intervals of 4 until you arrive at 125 common decks as the maximum. The customer can get exactly a certain number of triumph decks vs. common decks only by picking a number of triumph decks divisible by 4, or a number of common decks divisible by 5.

His final step is to calculate the number of cards per deck given various numbers of cards per suit, between 8 and 16.

Not surprisingly, there are 4 times the cards per suit in common decks and 5 times in triumph decks. The ratio of 4/5 applies within the decks as well as between decks. The point is to show that the customer with this arrangement has considerable choice and flexibility in what decks to order, and how many cards per deck.

The only remaining issue that he goes into, briefly, is that it is not clear that the number of cards in a common deck is always the same, in practice, as the number of regular suit cards in the corresponding triumph deck. On that slightly disturbing note he ends the article. He has got what he wanted, a plausible number for triumph decks as implied by the contract reported by Orioli; this is because he thiks that 12 triumph cards per triumph deck or fewer is too low, based on what what little we know about the various tarot sequences, and that 14 is better. That 16 also works is some comfort, however, given what we know about the Cary-Yale.

Now I want to explain why I find Franco’s argument completely unconvincing. In essence, I see no reason using what happens when X = 0, i.e. there are only triumph decks, as a basis for what follows. The contractor is not asking for all triumph decks, but for a mixture of the two, and it happens that in such mixtures there are more possibilities for making the decks come out even than just that of a ratio 4/5 of cards in a common deck to cards in a triumph deck. However the result is either one that gives much less flexibility in the ratio of common decks to triumph decks that can be requested, or one that does not conform to the “plausible” numbers that Franco picked for his demonstration, based on what little we know. The operative word here is “little”, unfortunately. Also, Franco did not explore other plausible options, as he recognizes.

I will illustrate. Orioli had the suggestion of common decks with 40 cards and triumphs decks with 60. If so, that would be 20 cards particular to the tarot sequence. That is indeed a number that has been suggested for the tarot sequence: it could be the 22 minus the Tower and Devil cards, as we see in all the surviving PMB and PMB-clone cards, which, in the form we have them (i.e. with the 2nd artist cards), are probably of the same era as 1477 Bologna. Now it is easy to get numbers for triumph and common decks with such composition. We start with 125 common decks. If we change 3 of them to triumph decks, that will be 40 x 3 = 120 cards. For the same price we can have 2 truimph decks: 40 x 3 = 60 x 2. So with 122 common decks and 2 triumph decks, there are no cards left over. We can verify that with the formula that Franco gave at the beginning:

X Nc + Y Nt = 125 Nc
(122 x 40) + (2 x 60) = 125 x 40
4880 + 120 = 5000

Now our customer will probably want more than 2 triumph decks. Let us say that he sells three times as many common decks as he does triumph decks. If they had 40 cards, that would be around 31 of one and 94 of the other. But it is going to be fewer than 125 total, so fewer of each. We might guess 27 triumph decks. But that won’t work, because it isn’t divisible by 2. So let us guess 26. 26 triumph decks will take up 26x60 cards, equalling 1560. That equals 1560 divided by 40 common decks, i.e.. 39. Subtracting these 39 from 125 gives us 86 common decks and 26 triumph decks. 26 x 3 is 78, which isn’t enough triumph decks. 28 would give us 3 fewer common decks, i.e. 83. 28 x 3 = 84. So we go with 28 triumph decks and 83 common decks. Chccking our work:

28x60 + 83x40 = 125x40
1680 + 3320 = 5000

There is a formula our customer could have used, but to get it, one needs to know algebra, which I presume that our customer and card maker do not know. In that case, he is left with trial and error.

I will give another example that comes to the same thing. In Barcelona the composition of a regular deck around 1380 was given as 44 cards, according to Brunet y Bellet (viewtopic.php?f=11&t=1097&p=16954&hilit ... ona#p16954):

En 1’inventari de Nicoláu Sarmona, negociant de Barcelona, carrer de S. Daniel, any 1380 va continuat un «Ludus de naips qui sunt 44 pecie.

If that number was maintained in Bologna, and 22 more card were added to make a triumph decks, the ratio would be 44/66. That reduces to 2/3 and will have just as many possibilities for coming out even as the previous example. Again, a customer can get his 3 to 1 ratio by ordering 83 common decks and 28 triumph decks.

28x66 + 83x44 = 125x44
1848 + 3652 = 5500

It is also possible to order decks with any of the “plausible” combinations of common and triumph deck numbers in Franco’s first table. However there will be much less flexibility in quantities ordered. For example, for a 56 card common deck and a 78 card triumph deck, the ratio is 28 to 39. It will take 28 triumph decks to come out even. 28 triumph decks equals 39 common decks. So he will have to order 28, 56, or 84 triumph decks. If he orders 28 triumph decks, he will get 125-39 = 86 common decks, a ratio of close to 3 to 1.

For a 62 card triumph deck and 40 card common deck, the ratio is 31 to 20. The customer will have to order 20, 40, 60 or 80 triumph decks to come out even. With 20 triumph decks, he will get 125-39 = 86 common decks, a ratio of 4 to 1. With 40 triumph decks, he will get 125 - 78 = 47, close to even. 62 cards is not very flexible.

Another example is a 70 card triumph deck with a common deck of 48, as might be the case in Ferrara of 1457 (48 + 22). The ratio is 70 to 24. It will take 24 triumph decks to come out even; so our customer again does not have very many choices.

It is even possible to order 96 card triumph decks (assuming 56 cards in the common deck). The ratio is 96/56 = 12/7. He can order 7, 14, 21, 28, etc. triumph decks Let us try 28. 28 triumph decks uses up 28x96/56 = 48 common packs’ worth of cards, leaving 125 – 48 = 77 common decks. Well, that’s the best we can do. 21 would give 125 – (21x96/56) = 125 – 36 = 89, which is far more than 3 to 1.

A 97 card triumph deck is very inconvenient. The ratio is 97/56. It would take 56 triumph decks to make it come out even. 125 – 97 = 28 common decks. The customer would have to buy 97 triumph decks and 28 common decks.

97x56 + 28x56 = 125x56

At the end Franco brings up the issue that the common decks might not be simply the triumph decks minus the special triumph cards. That is no problem; the math works the same. Let us say that there are 48 card common decks and 96 card triumph decks (as might be the case for the Rosenwald). The ratio is 1/2, by far the most favorable yet. You can order any number of triumph decks you like (as long as you don't go over 48x125 cards total), and the result will come out even. Let us try 24 triumph decks. Then there are 125 – (24x96/48) = 77 common decks. That is close. But 25 triumph decks would be 125 – (25x96/48) = 75. That is exactly what we wanted.

In conclusion, almost anything works, given Alioli’s figures, depending on how flexible you can be. The lower the number in numerator of the ratio of common decks and triumph decks, the more flexible you can be. The ratio of 4 to 5 is not bad, and if the customer wants to make nothing but triumph decks, but for some reason expressed in a contract that is in terms of common decks and precisely 125 of them, it would be the best. But for mixed orders, common and triumph decks, a ratio of 2 to 3 is even better. Making for much less flexibility are both a 62 and a 78 card triumph deck. Thus Orioli's numbers of 40 and 60 are plausible. 48 and 96 offer the most flexibility of all, but I would have expected the word "minchiate" or "germini" to be used. I am left wondering if the tarocchino deck might not have originally been 66 cards, in which case a 22 card tarot sequence with 11 cards per regular suit might well have been invented by Prince Fibbia. Nah, of course not.

Some earlier material to the document:

http://trionfi.com/0/l/51-bologna/
http://trionfi.com/0/e/35/

Note Ross Caldwell: The article by Emilio Orioli "Sulle carte da giuoco a Bologna nel secolo XV" is from the Italian journal "Il libro e la stampa" n.s. 2, fasc. 4-5 (1908) pp. 109-119. It is online at the website of the "Emeroteca Digitale"
http://emeroteca.braidense.it/eva/sfogl ... olo=276349

The text, which is focussed by Franco Pratesi and translated by Michael S. Howard ...

Item che el prefato ser Roberto sia obligato dare e pagare al prefato maestro Pietro o a suo figliolo in suo nome soldi diexedotto de quattrini per ogni centovinticinque para de carte, o vero triumphi para tanto manco de centovinticinque para, quanto gette el numero de le carte che ha più li iochi de li triumphi da quilli de le carte.

(Item that the aforesaid Mr. Roberto is obligated to give and pay to the aforesaid Master Pietro or his son in his name eighteen soldi of money for each 125 packs of cards, or true triumphs sufficiently less than for 125 packs, in so far as the number of the cards is more of Triumphs than of cards.)

... is marked by me with red signs.

I get problems with this text. I don't know, what 18 soldi in Bologna precisely means in comparison to the Florentine money, but if I assume, that it is somehow in the range of 18 soldi in Florence, then my own logic about the playing card prices strikes. 18 soldi for 125 decks is too far below the prices, which the silk dealers paid for the decks of Niccolo di Calvello, who made the cheapest decks in Florence in the 1440s/50s. How shall this be possible?

18/125 = 0.144, which would be about 1.5 denari for a deck

As far I understood the whole operation, it's a contract for a future cooperation, maybe that's a payment before action, a deposit or prepayment, possibly for the paper, which must be bought before production. In the earlier text I see a "250", and 2x125= 250, possibly there's a relation between these both numbers.

Yes, good question. Besides the 250, there is also an earlier reference to "diexedotto misi", whatever that means. It bears looking at.

It just occurred to me that one argument in favor of 4/5 might still be the number 125 in particular, which on my account has no special significance; but it could if there was some special association between triumph decks and the number 100. If there is, and 125 is the number chosen for common decks, then the ratio between the sizes of the two decks is suggested as 4/5. But I don't know anything special about 100 for triumphs, or 125 for common decks.

Franco wrote me that he would like to know if from my perspective I could produce tables similar to the ones he produced, i.e. the one that had 0-100-100 on top and 125-0-125 on the bottom, except for different ratios of common decks to triumph decks. I thought that was a good idea, if only to double check the soundness of the argument. I have produced 4 such tables, for 4 different ratios, 2 at opposite ends of the spectrum and 2 in the middle. That should be sufficient to show that in every case, up to the limit of 125Nc total cards, it will be possible to construct such a table. Of course there will be, in all my examples, one row of the table blank, namely the case where only triumph decks are produced. But this was a case explicitly excluded from the contract.

First, for Orioli's 40 common cards, 60 triumphs example:






If you count them, you will find that there are 41 choices, plus the choice of all common decks, as opposed to 26 in the case of the 4/5 ratio. This will be the same for any 2/3 ratio deck. And this is not the ratio that gives the maximum number of choices. For 48/96 ratio decks, and anything with a ratio of 1/2, there will be 63 choices, i.e. one more than half the number of common decks. The final choice will be 62 triumph decks plus 1 common deck. That doesn't include the choice of all common decks, so with that one there will be 63 choices.

Now for my second example, at the other extreme, a 97 card triumph deck with a 56 card common deck. so a 56/97 ratio.





If the customer wants more common decks to go with his 56 triumph decks, he will have to order 125 of them for a double order, for a total of 56 triumph decks and 153 common decks.

My third example is the 62 card triumph deck along with 40 card common decks. His choices are below:





These are not very many choices, but at least there is more than one, and they offer come variety.

A 78 card triumph, 40 to 56 card common deck will offer similar choices, except with the 48 card common deck, which will offer two or thee times more. For 48 common card decks, the ratio will be 8/13, vs. 20, 22, 26, or 28 over 39 for the others; it is the numerator that is decisive, while the denominator affects how low the numerator can be. Here are the choices for 78 triumph and 48 common card decks.


There are 10 choices, as opposed to 4 with the 40 card common pack, or 9 and 3 without the all-common card decks choice. That is not 41 or 42, but it is better than 3 or 4.

For my part I've a problem with the connected price.

The problem with the number of cards becomes easier, if you reduce it to used woodblocks. If you set the relation between trumps and normal cards to 1:4, you best deal with 4 woodblocks for normal cards and 1 for trumps, or 8 and 2, if the cards are larger. If the relation is 1:2 (as in 40/60 as suggested by Orioli, which actually is 20:40), you have solution with 3 and 6 woodblocks.

In the case of Tarocchino 40+22, one could use woodblocks with 3x7 = 21 cards for one block and with 3 blocks (3x21=63) with the loss of one free place (which can be used for a free additional deck card, advertising for the producer or whatever).

The price is the problem. If the 125 is only related to the paper costs the operation becomes different, possibly not connected to the 1:4 choice. 125 is also 1/8 of 1000, possibly the usual calculation with dozens was broken in this contract.
... .-) ... that would be bad for the 5x14-theory, but it's better to have an accurate calculation. Somehow it seems necessary, that one has the full document translated.

The document is very difficult for me, due to the archaic words, spelling, and font. I have a very rough translation of the whole thing which still doesn't make complete sense. So what I will do is quote everything relevant at http://trionfi.com/0/e/35/, including the corresponding part of the contract, on three aspects of the customer's (Roberto Blanchelli's) obligation to the master card maker Piero:

(1) Roberto provides the paper. Here I first quote the Accedemia del Tarocchino Bolognese, which you cite at the above link:

Il figlio di Bonozzi s'impegnava a fabbricare per diciotto mesi in esclusiva per Blanchelli carte e trionfi su carta fornita dal committente.

(The son of Bonozzi undertook to manufacture for eighteen months, exclusively for Blanchelli, cards and triumphs on paper supplied by the client.)

Oriolo, at the same link:

...prometteva invece che per lo spazio di diciotto mesi continui si sarebbe dedicato a preparare carte e trionfi unicamente per conto del Blanchelli; il quale a sua volta, doveva fornire la carta ed i cartoni necessari per fare "dicte carte o vero triumphi".

(...he [Piero] promised instead that in the space of eighteen continuous months he would devote himself to prepare cards and triumphs solely on behalf of Blanchelli; who in turn, had to provide the paper and cardboard [boxes?] needed to make "said cards or true triumphs".)

And in the contract itself:

Item chel prefato ser Roberto sia obligato dare al prefato maestro Piero o a suo figliolo predicto tutte le carte e cartuni che andaranno per fare dicte carte o vero triumphi secondo el consueto e segondo quello che se le fara overo dira qualunche altro maestro de simile misterio a tutte sue proprie spese.

(Item, that the aforesaid Mr. Roberto is obligated to give the aforesaid master Piero or his aforesaid son all the cards and cardboard that go to make said cards or true Triumphs, according to the usual and according to to what others master of similar craft will do or say, to all his own expense.)

(2) Roberto pays 18 soldi for every 125 packs, for expenses such as ink, eggs, coloring, and other things. Here is Orioli:

Oltre la mercede convenuta doveva anche il Blanchelli aggiungere soldi diciotto a titulo di spese, ogni centoventi mazzi di carte o per altrettanti di mazzi di trionfi correspondenti; ... . Per le spese quindi dovevasi tener coto non dei mazzi, ma del numero delle carte, che effettivamente occorrevano per formarli; il diciotto soldi che i Blanchelli si obbligava a pagare in piu, a titolo di spese, dovevano poi servire per l'acquisto di "verzino, vederamo, agiuro, colla, alume de roza, inchiostro per fare dicte carte o triumphi".

(Besides the agreed upon award Blanchelli also had to add eighteen soldi dedicated to expenses, for each hundred and twenty-five decks of cards or likewise packs of corresponding true triumph cards... For expenditure therefore takes into account not packs, but the number of cards that actually it takes to form them; the eighteen soldi that Blanchelli is obliged to pay in addition, by way of expenses, were then to be used to purchase "verzino, vederamo, agiuro, glue, alum de roza, ink to make said cards or Triumphs".)

And the contract:

Item che el prefato ser Roberto sia obligato dare e pagare al prefato maestro Piero o a suo filiolo in sao nome soldi diesedotto de quattrini per ogni centovincinque para de carte, o vero triumphi para tanto manco de centovinticinque para, quanto gette el numero de la carte che he piu li jochi de li triumphi da quilli de le carte. E quisti soldi diexedotto sonno per vergino, verderamo, agiurro, colla, ove, alum de roza inchiostro per colori e generalmente per ogne altre spese che podesse andare in fare dicte carte o triumphi, li quali decedotto soldi pagati a prefato maestro Piero sia obligato farle poi li fare a tutte sue spese de le caret e cartuni infuore le quale esso ser Roberto glie debia dare e pagare como di sopra.

(Item: that the aforesaid Mr. Roberto is obligated to give and pay the aforesaid master Piero or his son in his name 18 soldi of money for each 125 packs of cards, or true Triumph packs of less than 125 packs, no matter if the number of cards is more for playing cards or Triumphs. And this 18 soldi is for vergino, verderamo, agiurro, glue, eggs, alum de roza ink for coloring and generally for all other expenses that could go into making said cards or Triumphs, 18 soldi paid to aforesaid master Piero is obligated to make then at his own expense the cards and cartuni infuore [packing cases?] which this ser Roberto must give and pay him as above.)

(3) Roberto pays Piero or his son 5 lire bolognini for every 125 packs produced. Orioli leaves out this part, which is your main concern.

Contract (beginning of last paragraph):

Item chel prefato ser Roberto sia obligato dare e pagare el prefato maestro Piero o vero a so figlilo, piacendo a lui, per ogni cento vinticinque para de carte che lui glie fara fare, o vero triumphi, a rata per rata del numero de le carte como di sopra Lire cinque de bolognini de moneta corente e quisti per la sua fatica e mistiero che durara dicto suo figliolo in farli fare dicte carte e triumphi;

(Item that aforesaid ser Roberto is obligated to give and pay aforesaid el maestro Piero or true to his son, if it pleases him, for every 125 packs of cards, or Triumphs, that he will make, payment according to the number of cards as above, five Lire bolognini of current money and this for the effort and expertise his son endures and in making said cards and Triumphs;...)

There is more about the five lire, but I don't think it contradicts what is said here. I hope this helps.

Well, we don't know, how the Bolognese money relates to the Florentine money. The deal is simply 1 Bolognese Lira for the work alone (nothing else, anything else is paid by the commissioner) with 25 "normal decks".

If Trionfi cards were added, the number of cards produced as triumphs was subtracted from the cards necessary for the normal 25 decks (which somehow says, that the Triumph cards didn't make more work as single cards than single cards of normal decks in this type of production process).

I would think, that cardboard in this context means the woodcut blocks. The commissioner just hired the work on the decks and gave all material (or paid for some material with 18 soldi for 125 packs).

Then I would say, that the number "125" came possibly from the basic deal "1 Lira for 25 decks" ... and the 125 was chosen, that one hadn't to transport the decks too often, but in a ruled way. The commissioner could order the group of decks after his experience in selling them. If Trionfi cards sold better than expected, he could increase the number, if they sold bad, he could decrease the number.
So one cannot conclude, that 125 points to 100 possible Trionfi decks or to a 1:4 relation between trumps and normal cards.

On the other hand we have the indicated value "that the Triumph cards didn't make more work as single cards than single cards of normal decks in this type of production process". If all woodblocks would have the same size and number of cards, then it would be true (this is given with 20 : 40, as Orioli suggested [3 woodcut boards], and it would be also true in the 1 : 4 relation [5 woodcut boards]). If the trump woodcut boards for trumps would be smaller than the others, then it would be more work, and if the woodcut boards for trumps would be larger, it probably would be less work, just cause the number of printing processes would increase or decrease.

Anyway, I think, it stays some doubt, and we cannot count the document as evidence for the 5x14-theory. How did Orioli come to his 20 : 40 relation? It doesn't fit with Tarocchino. If it isn't in the document, perhaps he concluded in a similar way: 3 woodcuts are necessary for this.

Huck wrote

So one cannot conclude, that 125 points to 100 possible Trionfi decks or to a 1:4 relation between trumps and normal cards ...Anyway, I think, it stays some doubt, and we cannot count the document as evidence for the 5x14-theory.."

That seems to be Franco's conclusion, too. He writes (email of Dec. 3, 2016)

In this particular case, I am somewhat glad to have been found to be wrong. Indeed, the year 1477 appeared too late for a 5x14 or a similar pack, and it could probably only be coherent with some unknown local habit.

Huck wrote,

I would think, that cardboard in this context means the woodcut blocks. The commissioner just hired the work on the decks and gave all material (or paid for some material with 18 soldi for 125 packs).

Using the search word "cartoni" in this forum, I get 5 responses. The first is a quotation from Bellosi at viewtopic.php?f=11&t=964&p=14016&hilit=cartoni#p14016. He says:

Sono pittori che troviamo impegnati a dipingere carte da tarocchi, a preparare disegni per ricami, ad eseguire affreschi poveri in terretta verde, a colorare e dipingere rilievi in stucco o in terracotta, a disegnare carte da gioco per la stampa, a mettere in opera cartoni per vetrate (magari su disegno di artisti più importanti di loro), ma soprattutto impegnati a dipingere "cofani" (cioè cassoni), spalliere e deschi da parto, rispondendo alle esigenze di una moda che si era largamente diffusa nella Firenze del Quattrocento tra le famiglie facoltose.

(They are painters who are busy painting tarot cards, preparing designs for embroidery, executing frescoes in poor green terretta, coloring and painting reliefs in terracotta or stucco, drawing playing cards for printing, putting in place cartoons for stained glass windows (perhaps designed by artists more important than they), but especially busy painting "cafoni" (i.e. cassoni), headboards and birth trays, meeting the demands of fashion that were widespread in fifteenth-century Florence among wealthy families.)

My guess was "cartoons", since they are for stained glass windows.

The next is Gnaccolini in her essay on the Sola-Busca (viewtopic.php?f=11&t=988&p=14716&hilit=cartoni#p14716)

125. Dalla radice greca della parola potrebbe indicare "ciò che sta sotto", quindi un essere infernale. Il diavolo è raffigurato in veste di frate ad esempio nella vetrata neotestamentaria del duomo di Milano realizzata su cartoni di Vincenzo Foppa: ill. in Pirina 1986, p. 181. Si tratta invece dell'Eremita secondo Dummett 1993, pp. 80 n. 6, 136.

(125. From the Greek root of the word, it could mean "that which is below", thus an infernal being. The devil is depicted as a monk, for example, in the New Testament window of Milan cathedral realized on cartoons by Vincenzo Foppa: ill. in Pirina 1986, p. 181. It is instead the Hermit according to Dummett 1993, pp. 80 n. 6,136.)

Both times it is for stained windows, and "cartoons" seems right.

Then in Dummett (viewtopic.php?f=11&t=1019&p=15211&hilit=cartoni#p15211)

Pertanto, alla fine del XVI secolo — e probabilmente molto prima di allora — si producevano mazzi di tarocchi sia a Lione che a Rouen. Essi venivano prodotti anche a Parigi; nei loro statuti del 1594, i maestri fabbricanti di carte di Parigi ripetutamente definivano la loro professione come quella di cartiers et faiseurs de cartes, tarotz, feuiletz et cartons (cartai e fabbricanti di carte, tarocchi, foglietti e cartoni) 7.

(Therefore, at the end of the sixteenth century - and probably long before then - Tarot decks were produced both in Lyon and Rouen. They were also produced in Paris; in their statutes of 1594, the master card makers of Paris repeatedly defined their profession such as cartiers et faiseurs de cartes, tarotz, feuilez et cartons (card makers and makers of cards, tarots, folios and cardboard) (7).)

Dummett is quoting from French. "Carton" in French means "cardboard" or "box" or "cardstock". A cartoon, i.e. preparatory drawing, is "esquise" or "croquis".

Then we have Franco Pratesi, at viewtopic.php?f=11&t=1074&p=16469&hilit=cartoni#p16469

Quindi troviamo una voce che è per noi di grande interesse, le 26 forme, che saranno discusse in seguito. Infine, cartoni e cassette varie.

(Then we find an item that is of great interest to us, the 26 templates [forme], which will be discussed later. Finally, various cartons and boxes.)

Here "cartoni" is definitely not woodblocks, which are called "forme". Here in the original of Dec. 1506 Florence, it is spelled "chartoni".

Finally there is Orioli in his summary of the contract:

Si obbligavva pure detto maestro Pietro a non permettere che suo figlio od alcuno altro de' suoi lavorasse o vendesse carte per altri, eccetto che per il Blanchelli, ne che aiutasse o consigliasse altri intorno a detto mestiere ne molto ineno lo insegnasse ad altri; prometteva invece che per lo spazio di diciotto inesi continui si sarebbe dedicato a preparare carte e trionfi unicamente per conto del Blanchelli; il quale a sua volta, doveva fornire la carta ed i cartoni necessari per fare "dicte carte o vero triumphi".

(It obliged also said Master Pietro not to let his son or any other to 'work on or sell their cards to others, except for the Blanchelli, or help or counsel others around said craft much less teach it to others; instead he promised that in the space of eighteen continuous months he would devote himself to preparing cards and triumphs solely on behalf of Blanchelli; who in turn, had to provide the paper and cardboard needed to make "dicte cards or true Triumphs.")

Orioli interprets "cartoni" as material used in making cards. This corresponds to the following in the contraxt.

Item chel prefato ser Roberto sia obligato dare al prefato maestro Piero o a suo figliolo predicto tutte le carte e cartuni che andaranno per fare dicte carte o vero triumphi secondo el consueto e segondo quello che se le fara overo dira qualunche altro maestro de simile misterio a tutte sue proprie spese.

(Item ,that the aforesaid ser Roberto is obligated to give the aforesaid Piero master or his aforesaid son all the paper and cartoni that go to make said cards or true Triumphs according the usual and according to what some other master of similar expertise will do or say, for all his own expense.

However the contract also says:

E quisti soldi diexedotto sonno per vergino, verderamo, agiurro, colla, ove, alum de roza inchiostro per colori e generalmente per ogne altre spese che podesse andare in fare dicte carte o triumphi, li quali decedotto soldi pagati a prefato maestro Piero sia obligato farle poi li fare a tutte sue spese de le carte e cartuni infuore le quale esso ser Roberto glie debia dare e pagare como di sopra.

(And this 18 soldi is for vergino, verderamo, agiurro, glue, eggs, alum de roza ink for coloring and generally for all other expenses that could go into making said cards or Triumphs, 18 soldi paid to aforesaid master Piero is obligated to make then at his own expense from the paper and cartuni infuore [packing cases?] which this ser Roberto must give and pay him as above.)

"infuore" might mean "outside."
In modern Italian cartoni (singular, cartone) can mean "boxes", "cardstock", "cardboard", or "cartoons"; in (http://www.wordreference.com/iten/cartone). Woodblocks are "forme" or "stampi" (singular "stampo"). "Cartoons" is possible, because for some of the packs, the contract might be calling fors for coats of arms on the backs, which would need designing for the cards. (I will discuss this passage later.) "Fuori" (outside, exterior) seems to be used in the context of these backs. However it might not be the backs, but rather on the boxes in which the cards are put, the cards themselves being white on the back. I need to figure out that part of the contract. (So it wouldn't be "packing cases", but rather "boxes".) Meanwhile, the use here seems closest to that in Franco's 1506 inventory, so "cartons" or "boxes" seems the most likely, and "cardstock" or "cartoons" next. But it is odd that woodblocks don't seem to be mentioned at all, as the responsibility of either party.

On Orioli's 20x40, I will work on a translation of what he says.

Note added later same day: I added the part where the contract says Roberto will furnish the cartoni, which I missed earlier. That affected my conclusion, which I rewrote accordingly (making it more ambiguous).

Huck wrote,

If all woodblocks would have the same size and number of cards, then it would be true (this is given with 20 : 40, as Orioli suggested [3 woodcut boards], and it would be also true in the 1 : 4 relation [5 woodcut boards]). If the trump woodcut boards for trumps would be smaller than the others, then it would be more work, and if the woodcut boards for trumps would be larger, it probably would be less work, just cause the number of printing processes would increase or decrease.
...How did Orioli come to his 20 : 40 relation? It doesn't fit with Tarocchino. If it isn't in the document, perhaps he concluded in a similar way: 3 woodcuts are necessary for this.

Here is Orioli, first as transcribed by Ross Caldwell at http://trionfi.com/0/e/35/; some of it is also in Andrea Vitali, Il Tarocchino da Bologna, p. 16, but he omits what is of interest to us (from "Ora per spiegarci questo passo" on). Then comes my translation. I have highlighted the relevant portion:

“Ma tornando alle carte da giuoco dipinte a mano, e degna di nota un contratto stipulato nel 1477 dal notaio Alberto Argellata fra un Roberto Blanchelli riminese, dimorante a Bologna e che era il committente, con maestro Pietro Bonozzi, mazziere degli anziani, il quale si obbligava con certi patti sopra "el mestiero de la carte e triumphi da zugare"; i quali patti dovevansi asservare dal figlio di lui, che s'impegnava versio il Blanchelli a provvedergli una certa quantita di carte da giuoco di due specie differenti. In questo contratto, oltre il prezzo pattuito, si stabiliva anche il modo come le carte dovessero essere lavorate, secondo un modello preparato e da conservarsi presso una terza persona; cbe se non fossero identiche o riuscissero eseguitite malamente, Pietro Bonozzi era obbligato a farle rifare; non dovevano avere sul dorso alcun disegno ma essere perfettamente bianche. Si obbligavva pure detto maestro Pietro a non permettere che suo figlio od alcuno altro de' suoi lavorasse o vendesse carte per altri, eccetto che per il Blanchelli, ne che aiutasse o consigliasse altri intorno a detto mestiere ne molto ineno lo insegnasse ad altri; prometteva invece che per lo spazio di diciotto inesi continui si sarebbe dedicato a preparare carte e trionfi unicamente per conto del Blanchelli; il quale a sua volta, doveva fornire la carta ed i cartoni necessari per fare "dicte carte o vero triumphi". Oltre la mercede convenuta doveva anche il Blanchelli aggiungere soldi diciotto a titulo di spese, ogni centoventi mazzi di carte o per altrettanti di mazzi di trionfi correspondenti, tenendo pero conto del maggior numero di pezzi che occorrevano per formame un mazzo, poiche "ha piu iochi de li triumphi da quelli de la carte". Ora per spiegarci questo passo, noi dobbiano tener presente la distinzione che si fa sempre in questo atto, fra "carte" e "trionfi". Colla parolla "carte" si intende il mazzo di carte usuali, formato di quaranta pezzi; invece la parola "trionfi", che vedemmo menzionato anche dal documento del 1459, sta a significara i "tarocchi bolognesi", ossia le carte cosi dette "lunghe", delle quali sappiamo che occorrono sessanta per formare il mazzo. Per le spese quindi dovevasi tener coto non dei mazzi, ma del numero delle carte, che effettivamente occoorrevano per formarli; il diciotto soldi che i Blanchelli si obbligava a pagare in piu, a titolo di spese, dovevano poi servire per l'acquisto di "verzino, vederamo, agiuro, colla, alume de roza, inchiostro per fare dicte carte o triumphi".

"But back to the cards from hand-painted game, and worthy of note a contract concluded in 1477 by the notary Alberto Argellata between a Roberto Blanchelli of Rimini, residing in Bologna, who was the client, with master Pietro Bonozzi, dealer of the elders, who is obliged with certain pacts concerning "the craft of playing cards and triumphs"; which pacts had to be fulfilled by his son, toward whom Blanchelli undertook to provide him with a certain quantity of playing cards of two different species. This contract, besides the agreed price, also established the way the cards were to be processed, according to a model [modello] prepared and kept by a third person; that if they were not identical or proved to be executed badly, Pietro Bonozzi was obliged to do them over; they should not have any design on the back but be perfectly white. It obliged also said Master Pietro not to let his son or any other to work on or sell their cards to others, except for Blanchelli, or help or counsel others around said craft much less teach it to others; instead he promised that in the space of eighteen continuous months he would devote himself to preparing cards and triumphs solely on behalf of Blanchelli; who in turn, he had to provide the paper and cardboard [cartoni] needed to make "said cards or true Triumphs". Besides the agreed upon reward Blanchelli had also to add eighteen soldi designated for expenses, for each hundred and twenty-five decks of cards or likewise packs of corresponding true triumphs, but taking into account the greater number of pieces needed for forming a pack, because "Triumphs has more of them than those of cards". Now to explain this passage, we must bear in mind the distinction that is always made in this act, between "cards" and "triumphs." The word "cards" means the usual pack of cards, formed of forty pieces; instead the word "triumph", which also is seen mentioned in the document of 1459, is to signify the "Bolognese tarot", i.e. the so-called "long” cards, of which we know that it takes sixty to form the deck. For expenditures therefore must be taken account not packs, but number of cards that it actually takes to form them; the eighteen soldi that Blanchelli is obliged to pay in addition, by way of expenses, were then to be used to purchase "verzino, vederamo, agiuro, glue, alum de roza, ink to make said cards or Triumphs".

About "long" cards, Italian wikipedia tells us:

Il tarocchino bolognese (in dialetto bolognese äl chèrt lónghi) è un gioco di carte derivato dai Tarocchi eliminando le carte numeriche dall'asso al cinque di ogni seme.

(The tarocchino bolognese (in Bolognese dialect "long cards") is a deck of cards derived from the Tarot eliminating the cards numbered from Ace to 5 in every suit.

However later on it is clear that the Ace is included in the deck. We see:

1.4.1 Danari e Coppe

Appartengono ai Semi detti CORTI e rispettano il seguente ordine gerarchico:

(FIGURE =) RE REGINA CAVALLO FANTE (SCARTINI =) ASSO 6 7 8 9 10

1.4.2 Spade e Bastoni

Appartengono ai Semi detti LUNGHI e rispettano il seguente ordine gerarchico:

FIGURE =) RE REGINA CAVALLO FANTE (SCARTINI =) 10 9 8 7 6 ASSO

Besides these are the 21 "numeri" (numbered) plus the Fool:

1.2 Ordine e grado gerarchico dei Trionfi

Le 22 carte dette Trionfi sono suddivise in 21 NUMERI e 1 MATTO.

So, 40 + 22 = 62. Or 78 - 16 = 62. I cannot get 60 however I do it. With the aces eliminated, too, it would be 58. I have no idea what Orioli was thinking of. Perhaps it is a typo in Orioli's text, which he missed.